Задания
Версия для печати и копирования в MS WordДоказать, что существует не менее пяти различных разбиений прямоугольной доски на пять треугольников, из которых можно сложить квадрат.
Решение. 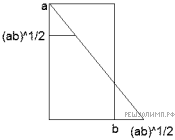
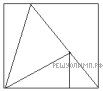
Разделим прямоугольник на два треугольника и пятиугольник, как указано на рисунке. Очевидно, из них можно сложить квадрат. Тогда остается произвольно разбить пятиугольник на три треугольника. Это можно сделать пятью способами (по числу вершин, в каждом способе из вершины проводим два отрезка к несмежным вершинам).
?
Межрегиональная олимпиада школьников по математике САММАТ, 10 класс, 2 тур (заключительный), 2018 годКлассификатор: Олимпиадная геометрия. Разрезания



