На каждой стороне правильного треугольника взято по точке. Каждая сторона треугольника с вершинами в этих точках перпендикулярна какой-либо стороне исходного треугольника. В каком отношении каждая из взятых точек делит сторону исходного треугольника? Каково отношение площадей исходного и образованного треугольников?
Решение. Пусть точки K, L, M лежат соответственно на сторонах AB, BC и AC правильного треугольника ABC, причем KL перпендикулярна BC, LM перпендикулярна AC и MK перпендикулярна AB.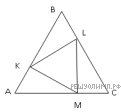
1) Тогда
Так же можно показать, что 
значит, треугольник KLM равносторонний. Прямоугольные треугольники AKM, BLK и CML равны по катету и острому углу, а так как
(как катет, лежащий против угла 30°), то 
Аналогично, 
и 
2) Пусть 
Тогда сторона исходного треугольника равна 
а сторона вписанного 
то есть в 
раз меньше. Поскольку площади равносторонних треугольников относятся друг к другу, как квадраты сторон, то площадь вписанного будет в 3 раза меньше.
Ответ: 1) 1 : 2; 2) 3 : 1.
Спрятать критерииКритерии проверки:| Каждая задача оценивается по 10-балльной шкале и снабжается отметкой в работе 0, −, ∓, ±, + в соответствии с критериями. |
| Вид погрешности или ошибки | Отметка в работе | Баллы |
|---|
| Решение задачи верное, выбран рациональный путь решения | + | 10 |
| Решение верное, но путь не рационален или имеются один — три недочета или негрубая ошибка | + | 9 |
| Решение верное, но путь не рационален и имеются один — три недочета или негрубая ошибка | ± | 7−8 |
| Ход решения верный, но есть несколько негрубых ошибок или решение не завершено | ∓ | 5−6 |
| Допущены грубые ошибки, но ответ получен (неверный) | ∓ | 3−4 |
| Допущены грубые ошибки и ответ не получен либо решение лишь начато, то что начато — без ошибок | − | 2 |
| Решение начато, но продвижение ничего не дает для результата | − | 1 |
| Задача не решилась | 0 | 0 |
| Недочеты: незначительные (непринципиальные) арифметические ошибки. Негрубые ошибки: технические ошибки в применении формул и теорем, не влияющие на смысл решения; необоснованность логических (верных) выводов. Грубые ошибки: I. Логические, приводящие к неверному заключению. II. Арифметические ошибки, искажающие смысл ответа. III. Неверный чертеж в геометрических задачах. IV. Принципиальные ошибки в применении элементарных формул и теорем. |
Ответ: 1) 1 : 2; 2) 3 : 1.
