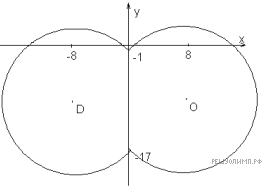
Рас­крыв знак мо­ду­ля и про­ве­дя пре­об­ра­зо­ва­ния, по­лу­ча­ем: при не­ра­вен­ство при­мет вид

при по­лу­чим не­ра­вен­ство

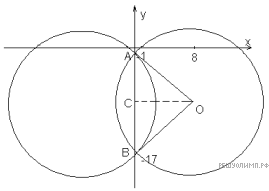
то есть фи­гу­ра, за­дан­ная ис­ход­ным не­ра­вен­ством имеет вид (см. левый рис.). Чтобы найти пло­щадь фи­гу­ры, про­ве­дем до­пол­ни­тель­ные по­стро­е­ния (см. пра­вый рис.).

Тогда пло­щадь фи­гу­ры можно найти по фор­му­ле:

Вы­чис­ля­ем пло­ща­ди, вхо­дя­щих в фор­му­лу объ­ек­тов:

Ра­ди­ус из­ве­стен, легко по­ка­зать, что OAB пря­мо­уголь­ный и рав­но­бед­рен­ный. На­хо­дим ис­ко­мую пло­щадь за­дан­ной фи­гу­ры:

Ответ: 704.