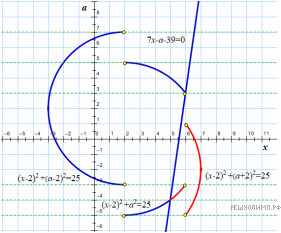
За­пи­шем ОД3: и Решим урав­не­ние по ча­стям:

1)  

2)  

Рас­кро­ем мо­ду­ли у вто­ро­го пунк­та:

а)  если то

б)  если то

в)  если то

В си­сте­ме ко­ор­ди­нат xOa по­стро­им гра­фи­ки по­лу­чен­ных функ­ций. От­ме­тим ОД3, это по­лу­плос­кость и точки, не при­над­ле­жа­щие пря­мым Пря­мые, па­рал­лель­ные оси Ox, пе­ре­се­ка­ют от­ме­чен­ные кри­вые ровно в двух точ­ках при

Ответ:

— при имеем ре­ше­ния

— при имеем ре­ше­ния