Задания
Версия для печати и копирования в MS WordВ треугольнике ABC проведены две высоты AA' и CC '. Найдите величину угла B, если известно, что
Решение. 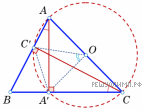
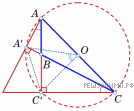
Спрятать критерии
Построим на стороне AC как на диаметре окружность, которая пройдет через точки A' и C', так как Из условия
следует, что отрезок A'C' равен радиусу построенной окружности. Значит, дуга, стягиваемая хордой A'C', составляет 60°. Отсюда угол C'CA', опирающийся на эту дугу, равен 30°.
Далее, если угол B — острый, то (см. левый рис.); если же угол B — тупой, то
(см. правый рис.), и, значит,
Ответ: 60° или 120°.



