РЕШУ ОЛИМП: задания, ответы, решения

Задания

Версия для печати и копирования в MS Word

Тип 0 № 7269 Добавить в вариант

Найти наибольшее значение функции

$y= дробь: числитель: 24 Пи x , знаменатель: левая круглая скобка 9 Пи в квадрате плюс 16 x в квадрате правая круглая скобка конец дроби$

на множестве решений уравнения

$синус x умножить на косинус 2 x минус 2 косинус в кубе x плюс косинус 2 x минус синус x плюс 2 косинус x=1.$

Спрятать решение

Решение.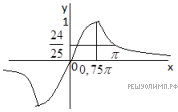

Преобразование:

$минус синус x умножить на левая круглая скобка 1 минус косинус 2 x правая круглая скобка плюс косинус x умножить на левая круглая скобка 2 минус 2 косинус в квадрате x правая круглая скобка минус левая круглая скобка 1 минус косинус 2 x правая круглая скобка =0 равносильно$
$равносильно минус синус x умножить на левая круглая скобка 1 минус косинус 2 x правая круглая скобка плюс косинус x умножить на левая круглая скобка 1 минус косинус 2 x правая круглая скобка минус левая круглая скобка 1 минус косинус 2 x правая круглая скобка =0 равносильно левая круглая скобка 1 минус косинус 2 x правая круглая скобка левая круглая скобка косинус x минус синус x минус 1 правая круглая скобка =0.$ $минус синус x умножить на левая круглая скобка 1 минус косинус 2 x правая круглая скобка плюс косинус x умножить на левая круглая скобка 2 минус 2 косинус в квадрате x правая круглая скобка минус левая круглая скобка 1 минус косинус 2 x правая круглая скобка =0 равносильно$
$равносильно минус синус x умножить на левая круглая скобка 1 минус косинус 2 x правая круглая скобка плюс косинус x умножить на левая круглая скобка 1 минус косинус 2 x правая круглая скобка минус левая круглая скобка 1 минус косинус 2 x правая круглая скобка =0 равносильно$
$равносильно левая круглая скобка 1 минус косинус 2 x правая круглая скобка левая круглая скобка косинус x минус синус x минус 1 правая круглая скобка =0.$

Множество решений:

$совокупность выражений косинус 2 x = 1 , косинус x минус \sn x = корень из: начало аргумента: 2 конец аргумента косинус левая круглая скобка x плюс дробь: числитель: Пи , знаменатель: 4 конец дроби правая круглая скобка = 1 конец совокупности . \Rightarrow совокупность выражений x = Пи k , косинус левая круглая скобка x плюс дробь: числитель: Пи , знаменатель: 4 конец дроби правая круглая скобка = косинус дробь: числитель: Пи , знаменатель: 4 конец дроби конец совокупности . \Rightarrow совокупность выражений x= Пи k, x=2 Пи m, x= минус дробь: числитель: Пи , знаменатель: 2 конец дроби плюс 2 Пи n, конец совокупности . n, m, k принадлежит Z .$ $совокупность выражений косинус 2 x = 1 , косинус x минус \sn x = корень из: начало аргумента: 2 конец аргумента косинус левая круглая скобка x плюс дробь: числитель: Пи , знаменатель: 4 конец дроби правая круглая скобка = 1 конец совокупности . \Rightarrow$
$\Rightarrow совокупность выражений x = Пи k , косинус левая круглая скобка x плюс дробь: числитель: Пи , знаменатель: 4 конец дроби правая круглая скобка = косинус дробь: числитель: Пи , знаменатель: 4 конец дроби конец совокупности . \Rightarrow совокупность выражений x= Пи k, x=2 Пи m, x= минус дробь: числитель: Пи , знаменатель: 2 конец дроби плюс 2 Пи n, конец совокупности . n, m, k принадлежит Z .$ $совокупность выражений косинус 2 x = 1 , косинус x минус \sn x = корень из: начало аргумента: 2 конец аргумента косинус левая круглая скобка x плюс дробь: числитель: Пи , знаменатель: 4 конец дроби правая круглая скобка = 1 конец совокупности . \Rightarrow$
$\Rightarrow совокупность выражений x = Пи k , косинус левая круглая скобка x плюс дробь: числитель: Пи , знаменатель: 4 конец дроби правая круглая скобка = косинус дробь: числитель: Пи , знаменатель: 4 конец дроби конец совокупности . \Rightarrow$
$\Rightarrow совокупность выражений x= Пи k, x=2 Пи m, x= минус дробь: числитель: Пи , знаменатель: 2 конец дроби плюс 2 Пи n, конец совокупности . n, m, k принадлежит Z .$

Наибольшее значение функции

$y= дробь: числитель: 24 Пи x, знаменатель: левая круглая скобка 9 Пи в квадрате плюс 16 x в квадрате правая круглая скобка конец дроби \Rightarrow y в степени левая круглая скобка \prime правая круглая скобка =24 Пи умножить на дробь: числитель: 9 Пи в квадрате минус 16 x в квадрате , знаменатель: левая круглая скобка 9 Пи в квадрате плюс 16 x в квадрате правая круглая скобка в квадрате конец дроби =0,$

следовательно, $x_\max = дробь: числитель: 3 Пи , знаменатель: 4 конец дроби$ и $y_\max =1;$ $x_\min = минус дробь: числитель: 3 Пи , знаменатель: 4 конец дроби$ и $y_\min = минус 1.$

Ближайшими к $x_\max = дробь: числитель: 3 Пи , знаменатель: 4 конец дроби$ решениями уравнения являются $x=0$ и $x= Пи ,$ причем на них достигается наибольшее значение функции y(x), $y левая круглая скобка 0 правая круглая скобка =0$ и $y левая круглая скобка Пи правая круглая скобка = дробь: числитель: 24, знаменатель: 25 конец дроби .$

Ответ: $y_\max = дробь: числитель: 24, знаменатель: 25 конец дроби =0,96.$

Олимпиада Росатом, 11 класс, 2 этап (заключительный), 2018 год

Классификатор: Алгебра: тригонометрия. Задачи о тригонометрических функциях, Методы алгебры. Преобразования выражений

Спрятать решение · Помощь