В некоторой стране 200 городов и 8 авиакомпаний. Каждые два города соединены рейсами одной из восьми авиакомпаний. Можно ли утверждать, что найдётся авиакомпания и больше 50 городов, между любыми двумя из которых можно добраться рейсами этой авиакомпании (возможно, с пересадками)?
Решение.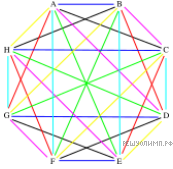 
Построим контрпример. Разобьём города на 8 групп по 25 городов. Назовём эти группы A, B, C, D, E, F и H.
Внутри каждой группы соединим города рейсами компании номер 1.
Компания номер 2 будет соединять города группы A с городами группы B, C с H, D с G, a E c F.
Компания номер 3 будет соединять города группы A с городами группы D, B с C, E с H, a F c G.
Компания номер 4 будет соединять города группы A с городами группы F, G с H, B с E, a C с D.
Компания номер 5 будет соединять города группы A с городами группы H, B с G, C с F, а E с D.
Компания номер 6 будет соединять города группы A с городами группы E, B с F, C с G, а D c H.
Компания номер 7 будет соединять города группы A с городами группы C, B с H, D с F, a E c G.
Компания номер 8 будет соединять города группы A с городами группы G, F с H, D с B, a E c C.
Таким образом, рейсы компании номер 1 связывают по 25 городов, а рейсы остальных компаний ровно по 50.
Это построение схематично изображено на рисунке. Разные компании обозначены разными цветами. Данный контрпример, разумеется, не единственный.
Ответ: Нет, это не обязательно верно.
Ответ: Нет, это не обязательно верно.
Аналоги к заданию № 740: 739 Все
