Трубчатый искусственный кристалл в поперечном сечении имеет фигуру, описываемую неравенством:

Построить это сечение и найти его площадь.
Решение. Неравенство  равносильно системе неравенств:
равносильно системе неравенств:

Решением неравенства  является множество точек, лежащих внутри круга радиусом
является множество точек, лежащих внутри круга радиусом  с центром в начале координат.
с центром в начале координат.
Рассмотрим неравенство 
1) Пусть 
 Тогда
Тогда

Решением этого неравенства является множество точек, лежащих вне круга радиусом

с центром в точке

2) Пусть 
 Тогда
Тогда

Решением этого неравенства является множество точек, лежащих вне круга радиусом

с центром в точке

3) Пусть 
 Тогда
Тогда

Решением этого неравенства является множество точек, лежащих внутри круга радиусом

с центром в точке

4) Пусть 
 Тогда
Тогда

Решением этого неравенства является множество точек, лежащих вне круга радиусом


с центром в точке

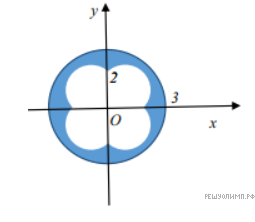
5) Изобразим на координатной плоскости сечение кристалла. Найдем площадь сечения (из площади большого круга вычитаем площадь фигуры, состоящей из 4-х половин маленьких кругов и квадрата).
Изобразим на координатной плоскости сечение кристалла (см. рис). Тогда получим, что площадь сечения равна: из площади большого круга радиусом  вычитаем площадь фигуры, состоящей из 4-х половин маленьких кругов радиусом
вычитаем площадь фигуры, состоящей из 4-х половин маленьких кругов радиусом  и квадрата со стороной
и квадрата со стороной  (т. Пифагора), т. е.
(т. Пифагора), т. е.

Ответ:  кв. ед.
кв. ед.
Спрятать критерииКритерии проверки:| Баллы | Критерии оценивания |
|---|
| 0 | Решение задачи неправильное и не содержит идей, с помощью которых задача может быть решена, или задача не решалась, или приведен верный ответ без обоснования |
| 1–4 | Задача не решена, но рассмотрены отдельные важные случаи при отсутствии решения (или при ошибочном решении) |
| 6–10 | Задача решена наполовину, т. е. ход решения правильный, есть значительный прогресс в решении, но полное решение требует дополнительных существенных идей |
| 12–14 | Задача решена в целом правильно и получен верный ответ, но есть мелкие замечания к решению (в решении допускаются незначительные неточности; имеются недостатки, которые легко устраняются) |
| 15 | Задача решена правильно, ход решения правильный и обоснованный |
Ответ:  кв. ед.
кв. ед.
равносильно системе неравенств:
является множество точек, лежащих внутри круга радиусом
с центром в начале координат.
Тогда
Тогда
Тогда
Тогда
вычитаем площадь фигуры, состоящей из
и квадрата со стороной
(т. Пифагора), т. е.
кв. ед.



