Найти все значения параметра a, при каждом из которых система неравенств
имеет хотя бы одно решение, и указать решения системы для каждого значения a.
Решение. Преобразуем систему к виду
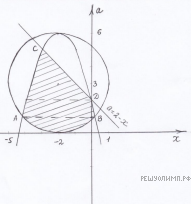
и начертим в одной системе координат в осях x, a графики ограничивающих искомую область линий: окружности
параболы 
и прямой 
(см. график).
Заштрихованная область на рисунке удовлетворяет всем условиям задачи. Найдём значения параметра, при которых графики пересекаются. Прямая и окружность:
соответствует тому, что вершина параболы лежит на окружности. Парабола и прямая:
отсюда 
и
Точка 
Система имеет хотя бы одно решение при 
Выразим x через a из уравнений окружности
и параболы 
Запишем ответ по графику.
Ответ: система имеет хотя бы одно решение при 
— при 
получаем 
— при 
получаем 
— при 
получаем 
— при 
получаем 
— при 
получаем 
Критерии проверки:| Баллы | Критерии выставления |
|---|
| 15 | Полное обоснованное решение. |
| 13 | Одна — две неправильно поставленные скобки (например, интервал вместо отрезка при выписывании решений). |
| 10 | Графики построены правильно, ход решения верный. Ответ незначительно отличается от правильного из-за арифметической ошибки при нахождении координат одной из точек пересечения графиков. Или небольшие ошибки (описки) при выписке решений. |
| 5 | Правильно найдены только значения параметра, при которых система имеет хотя бы одно решение. Сами решения в зависимости от параметра не указаны или указаны неверно. |
