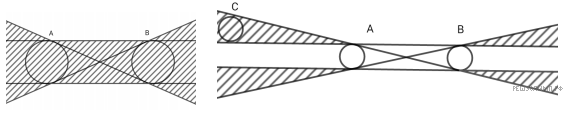
Решение. Начнем со следующего наблюдения: если даны два непересекающихся круга одинакового радиуса, то всевозможные прямые, пересекающие оба круга, заметают область, заштрихованную на рисунке слева. Эта область — объединение полосы между двумя внешними касательными к кругам и пары вертикальных углов между двумя внутренними касательными. Поэтому два данных круга A и B и некоторый третий круг C можно пересечь одной прямой тогда и только тогда, когда C имеет общие точки с заштрихованной областью. Будем называть эту область тенью кругов A и B.
Перейдем к решению задачи. Рассмотрим 2 cлучая.
Случай 1: любые 3 круга из заданного набора можно пересечь одной прямой. Тогда рассмотрим два круга A и B из набора, расстояние между центрами которых наибольшее. Если это расстояние меньше диаметра кругов, то прямая, проходящая через 2 общих точки граничных окружностей кругов A и B — искомая (любой круг C из набора обязан ее пересекать, иначе расстояние между центрами кругов A и C — либо B и C — окажется больше расстояния между центрами кругов A и B, что противоречило бы выбору кругов A и B). Поэтому будем считать, что расстояние между центрами кругов A и B больше диаметра, то есть эти круги не пересекаются.
Докажем, что тогда 4 общих касательных к A и B — искомые прямые, т. е. пересекают любой круг C из набора. Действительно, по предположению случая 1, круги A, B, C можно пересечь одной прямой. Тогда C должен пересекать тень A и B. Если бы C не пересекал ни одну из 4 общих касательных к A и B, то C целиком лежал бы в одном из 4 углов, заштрихованных на рисунке справа. Но тогда расстояние между центрами кругов A и C (либо B и C) было бы больше расстояния между центрами кругов A и B, так как центры трех кругов образуют тупоугольный треугольник. А это противоречило бы выбору кругов A и B. Значит, все круги набора можно пересечь 4 прямыми.
Случай 2: найдутся 3 круга из заданного набора, которые нельзя пересечь одной прямой. Тогда рассмотрим три таких круга A, B, C, центры которых образуют треугольник наибольшей площади. Докажем, что тогда 12 прямых — 4 общих касательных к A и B, 4 общих касательных к B и C, 4 общих касательных к C и A — искомые.
Предположим, что нашелся круг D из набора, не пересекающий ни одну из 12 касательных. По условию задачи, какие-то 3 из кругов A, B, C, D можно пересечь прямой. Пусть, без ограничения общности, это круги A, B, D. Тогда согласно наблюдению выше, D целиком лежит в одном из углов, заштрихованных на рисунке справа. Пусть, без ограничения общности, это “верхний” из углов, примыкающих к кругу A. C другой стороны, A, B, C нельзя пересечь прямой, значит, C целиком лежит вне тени A и B. Рассмотрим различные варианты расположения круга C.
Случай 2а: центры кругов C и D лежат в разных полуплоскостях относительно линии центров кругов A и B. Тогда центр круга A оказывается внутри треугольника с вершинами в центрах кругов B, C, D. При этом круги B, C, D также нельзя пересечь одной прямой: тень B и D расположена целиком “выше” нижней границы тени A и B, и не может пересечь круг C. Итак, мы получили 3 круга B, C, D, которые нельзя пересечь прямой, центры которых образуют треугольник большей площади, чем A, B, C. Это противоречит выбору кругов A, B, C.
Случай 2b: центры кругов C и D лежат в одной полуплоскости относительно линии центров кругов A и B, причем B и D лежат в одной полуплоскости относительно одной из общих внутренних касательных к B и C. Докажем, что в этом случае круги B, C, D нельзя пересечь прямой, а их центры снова образуют треугольник большей площади, чем A, B, C — тем самым снова придем к противоречию. Так как B и D лежат в одной полуплоскости относительно одной из общих внутренних касательных к B и C, то D не пересекает тень B и C, значит, B, C, D нельзя пересечь прямой. Треугольники с вершинами в центрах кругов A, B, C и B, C, D имеют общее основание BC, а высота больше у второго треугольника. Значит, последний имеет большую площадь. И в случае 2b мы пришли к противоречию.
Случай 2c: центры кругов C и D лежат в одной полуплоскости относительно линии центров кругов A и B, причем B и D лежат в разных полуплоскостях относительно обеих общих внутренних касательных к B и C. Докажем, что на этот раз круги A, C, D нельзя пересечь прямой, и уже их центры образуют треугольник большей площади, чем A, B, C. Первое утверждение следует из того, что D лежит вне тени A и C. Для доказательства второго утверждения проведем внутреннюю касательную к A и B, которая разделяет C и D, а также внутреннюю касательную к B и C, которая разделяет D и A. Будем катить круги A и C по своим касательным в сторону круга D до тех пор, пока они не коснутся обеих проведенных прямых одновременно. Будем двигать D в сторону B, пока он также не коснется обеих проведенных прямых. Ясно, что в процессе движение площадь треугольника A, B, C увеличивается, а A, C, D — уменьшается. А в конечном положении эти площади становятся равными, из симметрии. Значит, в исходном расположении центры кругов A, C, D образуют треугольник большей площади, чем A, B, C.
Итак, во всех случаях 2a–2c мы пришли к противоречию. Значит, любой круг D из набора пересекает хотя бы одну из указанных 12 прямых.



