Робот может совершать равные по длине шаги по дорожке вперед и назад, при этом выбор направления движения каждого шага является случайным и равновозможным. Робот сделал 10 шагов и остановился. Найти вероятность того, что он окажется на расстоянии более двух шагов от начала движения.
Решение. Если шагов всего один, то робот может остановиться в двух положениях, условно изображенных на рисунке.
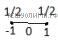
Здесь 0 — начало движения, −1 — шаг назад, 1 — шаг вперед. Вероятность попасть в положения −1 и 1 одинаковая и равна  Если шагов два, то существует три возможных положения робота в конце движения, условно обозначенных на рисунке.
Если шагов два, то существует три возможных положения робота в конце движения, условно обозначенных на рисунке.
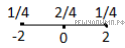
В положение −2 можно попасть из положения −1 после первого шага, совершив шаг назад. Таким образом, вероятность попадания в положение −2 за два шага равна  В положение 0 можно попасть из положений −1 и 1 после первого шага, совершив шаги вперед и назад соответственно. Тогда вероятность попадания в положение 0 после двух шагов равна
В положение 0 можно попасть из положений −1 и 1 после первого шага, совершив шаги вперед и назад соответственно. Тогда вероятность попадания в положение 0 после двух шагов равна

В положение 2 после второго шага возможно попасть только из положения 1, делая один шаг вперед. Вероятность попадания в 2 за два шага равна 
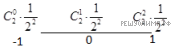
Далее образование коэффициентов при степенях  определяется треугольником Паскаля. Предположим, что робот сделал до остановки k шагов. Тогда существует
определяется треугольником Паскаля. Предположим, что робот сделал до остановки k шагов. Тогда существует  возможных положений, в которых он может остановиться. Крайние из них находятся на расстоянии k шагов от начального положения движения. Расстояние между соседними положениями равно двум шагам. На рис. изображены эти положения для четных и нечетных k.
возможных положений, в которых он может остановиться. Крайние из них находятся на расстоянии k шагов от начального положения движения. Расстояние между соседними положениями равно двум шагам. На рис. изображены эти положения для четных и нечетных k.
Для  вероятность остановки в положении равна
вероятность остановки в положении равна  в положении
в положении  (на расстоянии 2 шага от начала движения) эта вероятность равна
(на расстоянии 2 шага от начала движения) эта вероятность равна  в положение
в положение  (на расстоянии 4 шага от начального положения)
(на расстоянии 4 шага от начального положения)  и т. д. в положении
и т. д. в положении  эта вероятность равна
эта вероятность равна  В варианте
В варианте  Вероятность остановится в положении, отстоящем от начального не более двух шагов, равна
Вероятность остановится в положении, отстоящем от начального не более двух шагов, равна

а вероятность противоположного события  Для
Для  вероятность остановки в положении
вероятность остановки в положении  равна
равна  в положении
в положении  (на расстоянии 3 шага от начала движения) —
(на расстоянии 3 шага от начала движения) —  и т. д. остановка в положении
и т. д. остановка в положении  происходит с вероятностью
происходит с вероятностью 
Ответ: 
Ответ: 
длины 5 двигается на координатной плоскости так, что его концы лежат на параболе
Точка M — середина отрезка
Найти минимально возможное значение расстояния точки M до оси абсцисс, а также абсциссу точки M, при которой оно достигается.
Найти двугранный угол при основании пирамиды, если известно, что в усеченную пирамиду с плоскостями оснований P и Q можно вписать шар.



