Найдите все значения параметров a и b, при которых уравнение

имеет единственное решение если  при
при  и
и  при
при 
 Укажите это решение при каждом из найденных значение a и b.
Укажите это решение при каждом из найденных значение a и b.
Решение. Преобразуем исходное выражение:


Сделаем замену  Получим уравнение
Получим уравнение

Пусть при некотором значении параметра a это уравнение имеет единственное решение y0. Приходим к уравнению  Если
Если  то функция
то функция

на каждом промежутке

принимает все значения из интервала  (на каждом из указанных промежутков функция
(на каждом из указанных промежутков функция 
 принимает все значения, принадлежащие
принимает все значения, принадлежащие  а функция
а функция  ограничена). Таким образом, уравнение
ограничена). Таким образом, уравнение  при
при  будет иметь бесконечно решений, что не удовлетворяет условию задачи. При
будет иметь бесконечно решений, что не удовлетворяет условию задачи. При  имеем
имеем  решение единственное.
решение единственное.
Итак,  и необходимо выяснить, при каких a уравнение
и необходимо выяснить, при каких a уравнение

имеет единственное решение.
1) Если  то
то  то есть
то есть  Следовательно, при
Следовательно, при  уравнение имеет один отрицательный корень
уравнение имеет один отрицательный корень 
2) Если  то
то  Сделаем замену
Сделаем замену  приходим к уравнению
приходим к уравнению

Находим:
а) при  получаем
получаем  т. е.
т. е.  — единственное решение.
— единственное решение.
б) при  имеем квадратное уравнение, которое будет иметь два различных неотрицательных решения при следующих условиях
имеем квадратное уравнение, которое будет иметь два различных неотрицательных решения при следующих условиях

3) Уравнение (*) будет иметь одно неотрицательное решение,
3.1) если  тогда
тогда  Имеем
Имеем  и
и 
3.2) если

3.3) если

таких a нет.
Итак, при  уравнение (*) имеет ровно один неотрицательный корень
уравнение (*) имеет ровно один неотрицательный корень

и

При

уравнение (*) имеет ровно один неотрицательный корень

и

Совместим рассмотренные случаи:
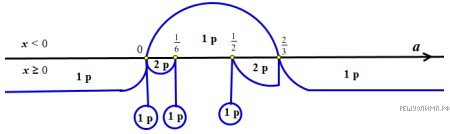
Ответ:
— при 


— при 


— при 


— при 





